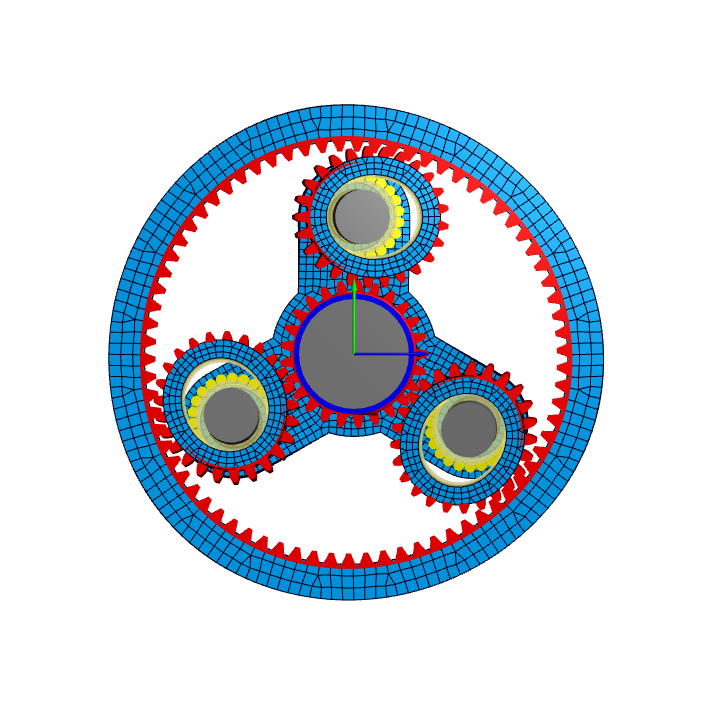
バージョン08/2016以降、MESYSシャフト計算ソフトウェアでは、3次元ソリッド要素としてモデル化された3次元弾性パーツと1次元ビーム要素として計算された弾性シャフトの連携が可能になっています。 3次元弾性パーツは、CAD形状をインポートするか、パラメータ入力によって定義することができます。
3次元弾性パーツは、シャフトモデルへのインターフェースで各々のノードに縮退されます。 ソフトウェアの次のバージョンでは、さらに歯車とベアリングの表面変形の結合が可能になります。 ハウジングの変形は、ベアリングリングの変形につながり、歯車の力は歯車ボディーの変形を引き起こします。最初の例は、図1に示す弾性歯車およびベアリング動輪を有する遊星歯車ステージです。
Figure 1: Planetary stage with 3D-elastic planet, ring and carrier
歯車の力は、歯車ボディーの変形をもたらし、歯車の歯が一様に変形していない場合、歯面の荷重分布に影響を与える可能性があります。 単純な軸の例における円筒歯車の線荷重分布に対する変形の影響を以下に示します。
この例は、中心に歯車を備えた2つの剛体サポートされたシャフトと、中心からわずかにずれた歯車を備えたシャフトです。
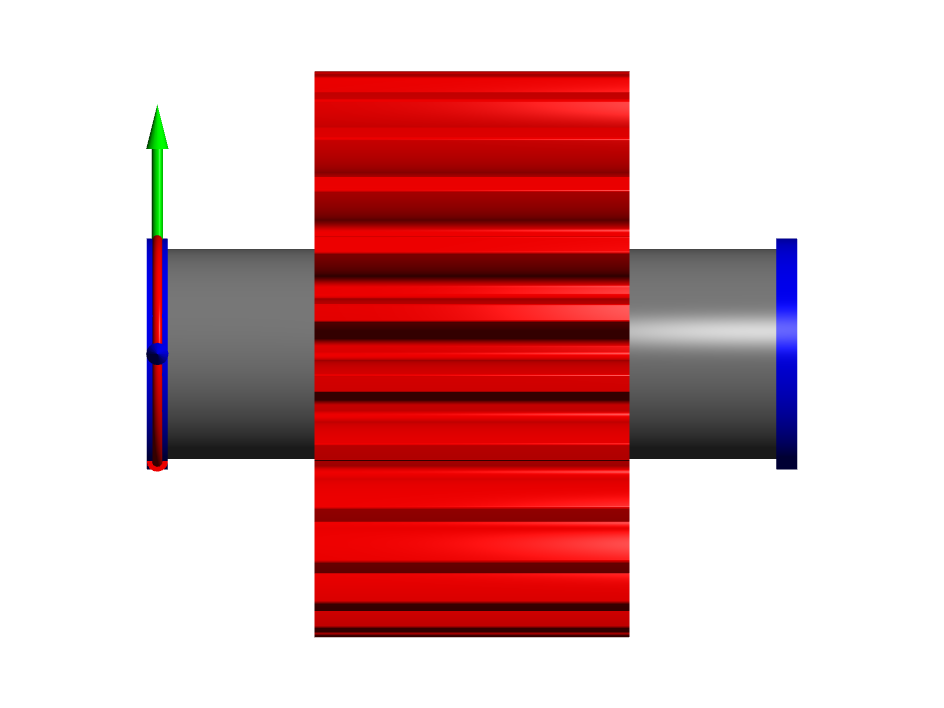
ISO 6336-1のセクション7.4.3.2では、曲げ変形の計算に対しては先端と根元の直径の平均値を使用し、ねじりの場合は根元の直径に0.4倍のモジュールを加えたものを使用することを提案しています。 ここでは、これら2つの間の48mm（z = 25、mn = 2の場合）の丸められた値がすべての計算に使用されます。 セクション7.4.3.3では、歯車としばりばめ接続のために、軸がハブ直径とボア直径との間の中間径によって補強されていることに留意します。 この平均直径は、シャフト変形の計算に使用できますが、以下の結果の通り、ギアの変形の計算には使用できません。
| Case | Image | Comment |
|---|---|---|
| 1 |  |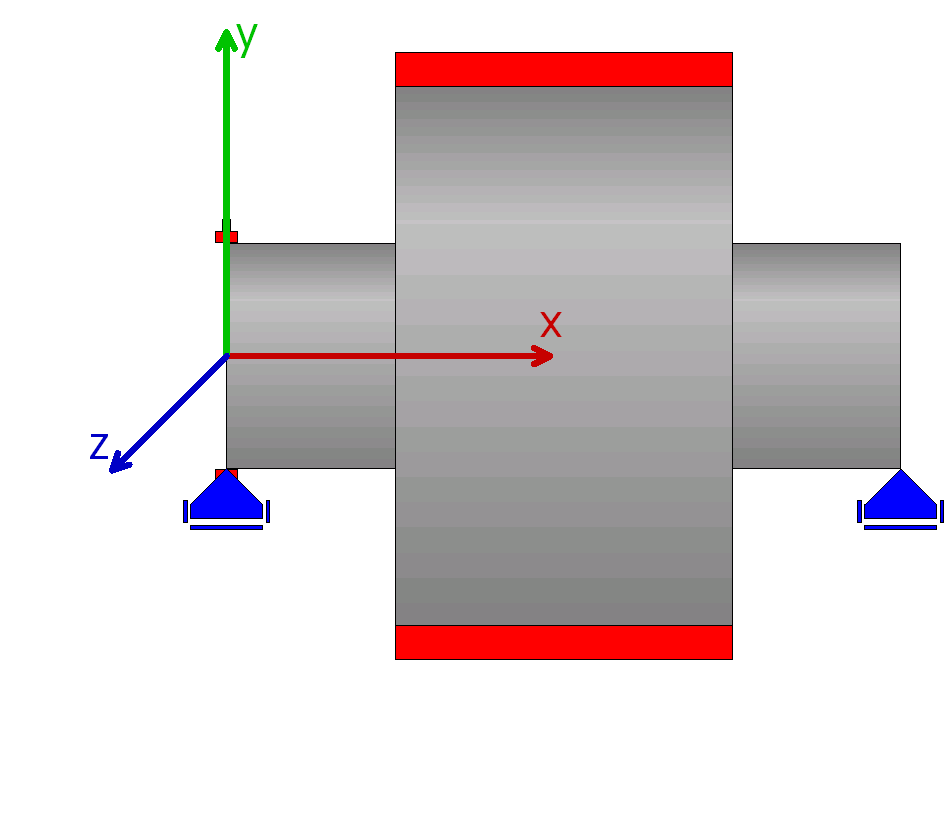
歯車の範囲部分の軸直径は、歯車の根元とピッチ直径との間の値を使用します。 |
| 2 |  |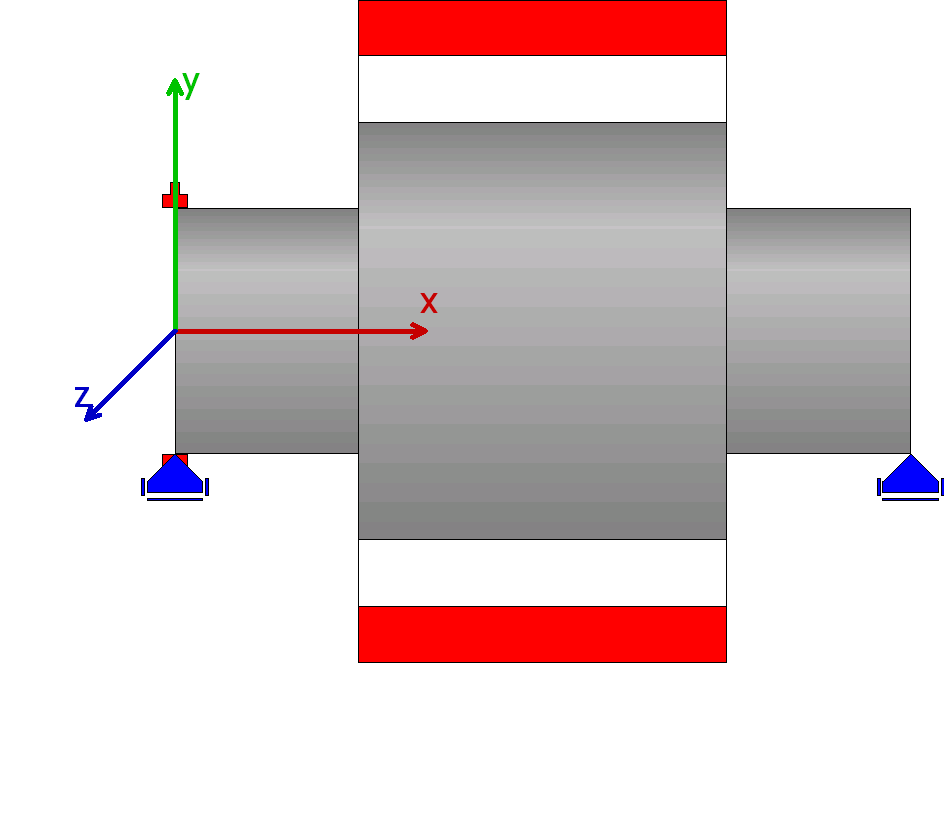
軸直径は、(20+48)/2=34mmの中間値を使用します。 |
| 3 |  |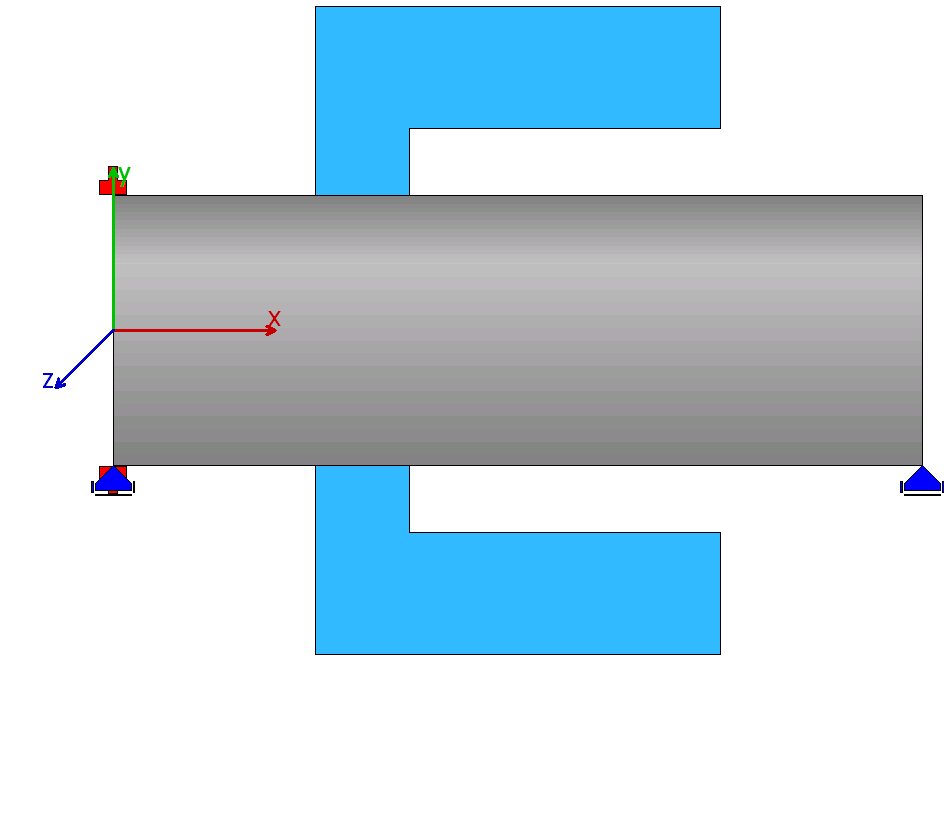
シャフトに左側で接続された、非対称の歯車本体が使用されます。 |
| 4 |  |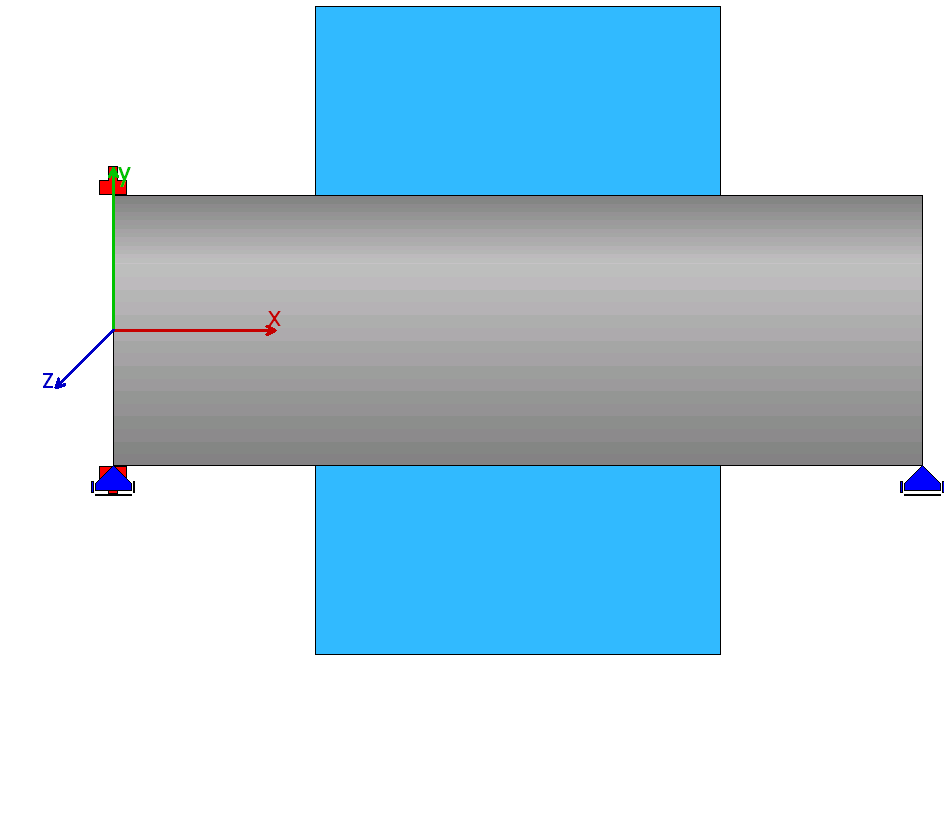
全ての円筒が歯車ボディーとして使用されます。 |
| 5 |  |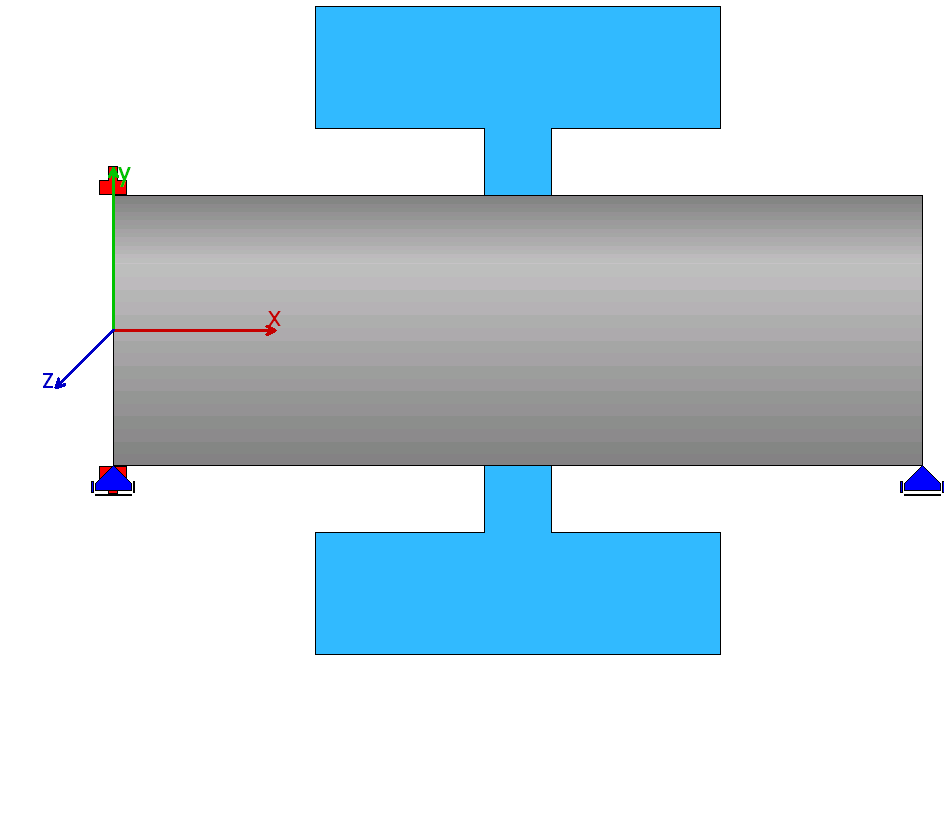
中心がリブ形状の歯車ボディー |
| 6 |  |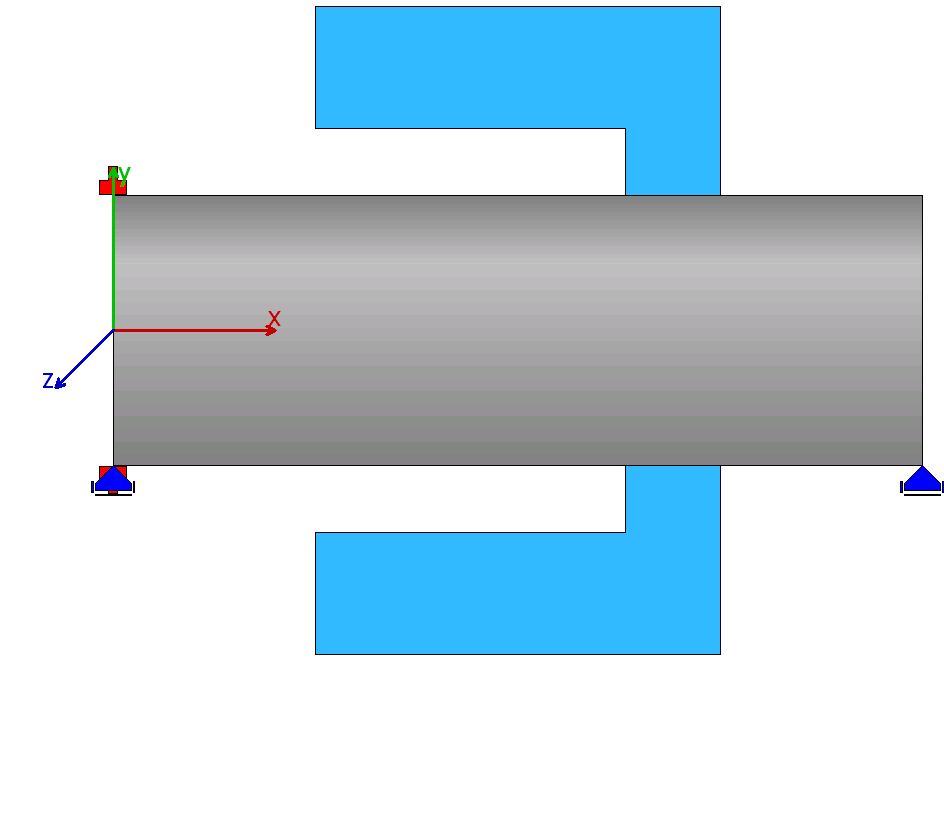
ケース3の対称形状で、右側にリブ形状。 |
歯車変形の計算のために、歯車は、全幅に亘ってしっかりと支持されている第2の剛性歯車と噛み合っています。 6つの例の歯車は全てこの中心歯車と接触し、シャフトの左側に導入された同じトルクで負荷されます。
Figure 3: Shaft system for the example
The results are shown for the centric gear and for the eccentric gear:
| Centric gear | 1 | 2 | 3 | 4 | 5 | 6 |
| Maximum shaft deflection [µm] | 6.5 | 8.3 | 26.1 | 9.8 | 26.8 | 26.1 |
| Line load wmax [N/mm] | 311 | 382 | 566 | 296 | 288 | 566 |
| Ratio wmax/wavg | 1.10 | 1.34 | 2.00 | 1.04 | 1.01 | 1.99 |
| Gap width [µm] | 1.6 | 6.0 | 27.6 | 0.8 | 0.0 | 27.6 |
| Eccentric gear | 1 | 2 | 3 | 4 | 5 | 6 |
| Maximum shaft deflection [µm] | 12.8 | 14.4 | 35.6 | 17.6 | 39.4 | 41.6 |
| Line load wmax [N/mm] | 350 | 423 | 630 | 339 | 333 | 535 |
| Ratio wmax/wavg | 1.23 | 1.49 | 2.22 | 1.19 | 1.17 | 1.89 |
| Gap width [µm] | 5.4 | 9.9 | 34.4 | 5.1 | 5.6 | 24.6 |
シャフトの最大曲げは、ギアのボディを考慮しないインナーシャフトになっておいます。荷重比wmax / wavgは面荷重係数と同様であるが、荷重依存効果のみが考慮され、製造誤差は考慮されない。支持体のたわみの製造公差の追加は、面荷重係数をより大きくします。ギャップ幅は、歯車を一点でのみ接触するまで仮想的に回転させることによって、フランクラインの変形から得られます。それは、フランクライン上の変形の量でなければなりません。
ケース1とケース4の両方とも全筒をギヤボディとして使用しています。ケース4のシャフト曲がりは、ケース1の場合よりも大きいですが、ギャップ幅やライン荷重が示すように、フランクラインの変形はより小さくなっています。これは、歯車本体の内部でシャフトが変形する可能性があるためです。一般に、ビームモデルは直径変化によって剛性が高くな過ぎます。したがって、ロータダイナミクスのための多くのプログラムは、直径変化に対して円錐の剛性直径を使用します。 3次元ソリッドモデルは、平均直径や円錐角を推測する必要なしに、これらの直径変化における応力分布を自動的に考慮します。
歯車本体の平均直径を用いたケース2は、ケース5との比較のように歯車の変形には有用ではありませんでした。しばりばめの場合、シャフトはケース5のようにギアによって補強されません。ケース5は、フランクライン上の変形がごくわずかでした。直径が小さくなるこのモデルは、ケース2がケース1よりも大きく、ケース4により近いように、シャフトの曲げラインの計算に役立ちます。
次の表は、中心位置およびずれた位置に歯車を配置した6つのケースのシャフトのたわみを示しています。図の縮尺が異なることに注意してください。
| Shaft bending | Centrical gear | Eccentrical gear |
|---|---|---|
| 1 |  |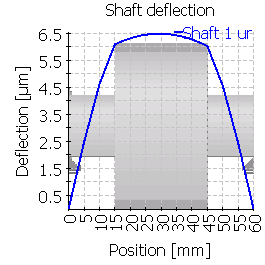
 |
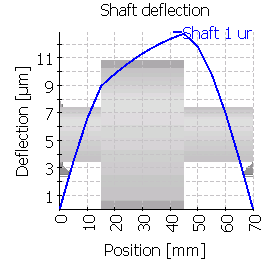| 2 |  |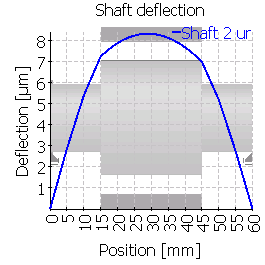
 |
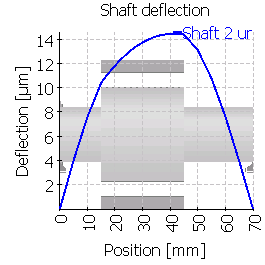| 3 |  |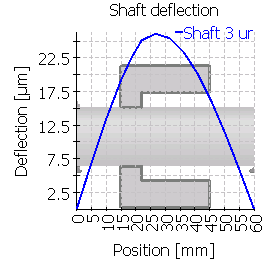
 |
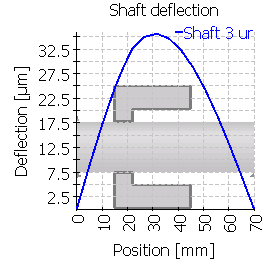| 4 |  |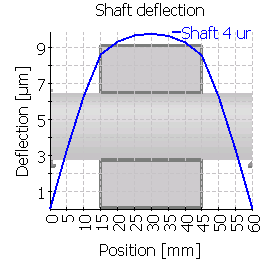
 |
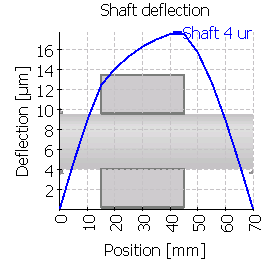| 5 |  |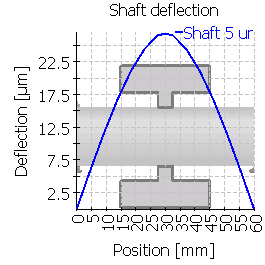
 |
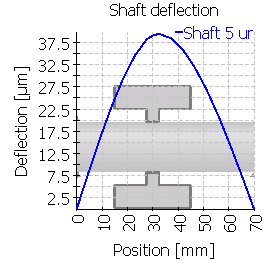| 6 |  |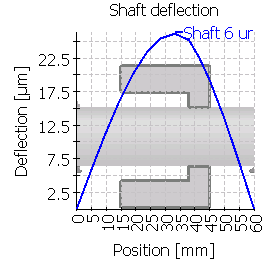
 |
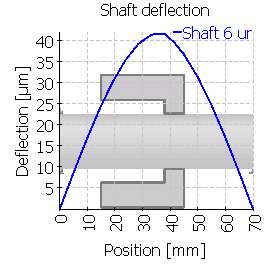次の表は、中心位置およびずれた位置に歯車を配置した6つのケースのライン荷重分布を示しています。
| Linienlast | Zentrisches Zahnrad | Exzentrisches Zahnrad |
|---|---|---|
| 1 |  |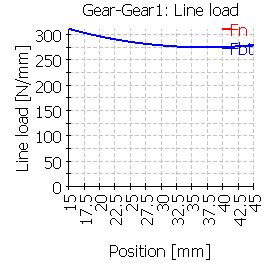
 |
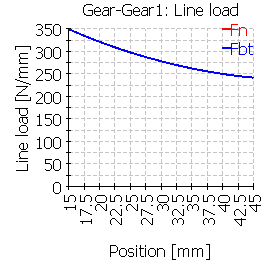| 2 |  |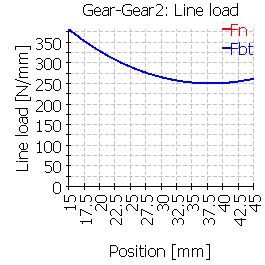
 |
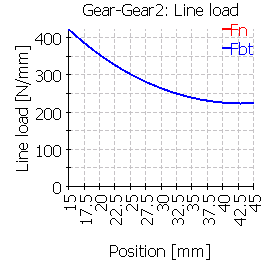| 3 |  |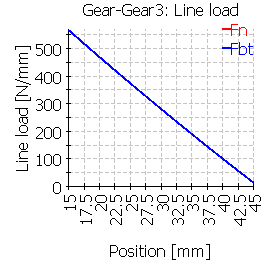
 |
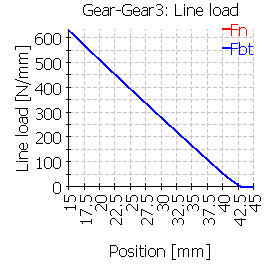| 4 |  |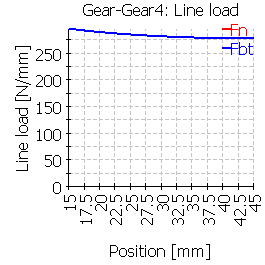
 |
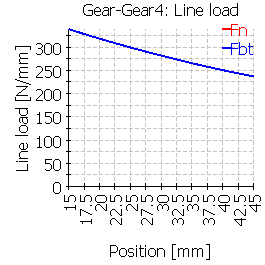| 5 |  |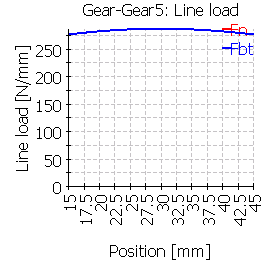
 |
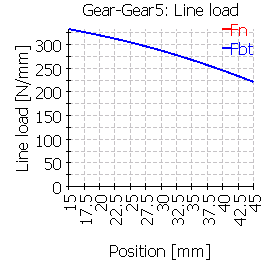| 6 |  |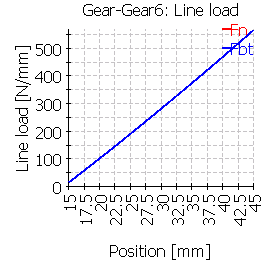
 |
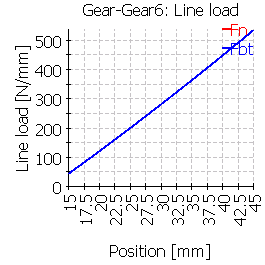ケース4とケース5を比較すると、ねじりの影響が小さいことが分かります。ケース4のソリッドシリンダでは、左からのトルクの影響が小さく見えますが、リブ形状のケース5は、ねじれや曲がりによる変形の外形の小さなクラウニングのような影響を示します。
ケース3と6は大きな不整合を示しています。ミスアライメントの主な理由は、軸受ボディの変形ではなく、大きな傾斜角の位置でのシャフトとの接続です。シャフトの傾斜角と歯車ボディーの変形は、これらの場合はギアフランク変形の合計され、他の場合は、より小さいシャフトのたわみ角になっています。
歯車本体のより詳細なモデルを使用することにより、シャフトのたわみおよび歯車のフランクライン変形の結果を改善することができます。シンプルなビームモデルを使用する必要がある場合は、歯車本体の外径をフランクライン変形の計算に使用する必要があります。シャフトのたわみの計算のためには、歯車本体のためのより小さい直径を使用することにより、シャフトの剛性のより良いモデルとなります。
これらの場合、最初一回の1分程度かかる歯車本体の静的な縮退の後、縮小された計算モデルでの計算時間はたった数秒です。唯一の欠点は計算ファイルのファイルサイズの増加です。
これらの例は、線荷重に対する変形の影響が示されるべきであるので、フランクライン補正なしで表されています。もちろん、フランクライン補正を含めて同じ計算を行うこともできます。