多くの場合、転がり軸受のラジアル方向またはアキシアル方向の剛性のために単一の値が使用されます。 いくつかの軸受タイプや負荷条件では、これは十分であるかもしれないが、他の場合はそうではないかも。
剛性とは何ですか? 一般に、剛性は、変位の変化に対する力の変化を表します。 力を変位で割ることc = F / uは、線形システムに対してのみ有効で、代わりに、与えられた動作点に対してc =ΔF/Δuのような勾配または差異を使用する必要があります。 転がり軸受の剛性は、すきまと転動体要素と軌道溝の間の非線形ヘルツ接触のために、非線形になります。
これは、ベアリング剛性の十分な定義ですか? 残念ながら違います。 剛体のベアリングリングを仮定すると、力またはモーメントによる3つの方向の変位と、2つの軸の周りの回転があります。 したがって、5 * 5の剛性マトリックスは25個の数を含んで定義されます。 FEAやローターダイナミクスの計算には、この完全な剛性マトリックスを使用するのが最善の方法です。
ラジアル剛性の単一の数値を定義する必要がある場合は、剛性マトリックスのy位置の主対角線は合理的な選択肢と思われますが、他の可能性もあります。 剛性マトリックスの主対角線は、固定された変位と回転ux、uz、ry、rzについてcyy =ΔFy/Δuyを計算するときに得られる剛性です。
cyy =ΔFy/Δuyを導き出す別の可能性は、固定された力Fx、Fzおよび固定されたモーメントMy、MzについてFyを変更して、Δuyを測定することでしょう。 あるいは、固定された力Fx、Fzと固定された傾斜角ry、rzを使ってcyy =ΔFy/Δuyを導き出すでしょう。
これらの方法のそれぞれは、異なるラジアル方向の剛性をもたらします。 接触角15°および軸力Fx = 500N、変動するラジアル方向の力Fyを有するアンギュラ玉軸受の場合、ラジアル方向の剛性cyy =ΔFy/Δuyについての以下の3つの値が導かれます。

ラジアル方向の剛性は、上部の2つの曲線では最初は減少しています。何故ならば、いくつかの転動体は、増加したラジアル荷重によって負荷が減少しているか、接触が緩んできているからです。
軸方向の剛性についても、同じことが計算されます:
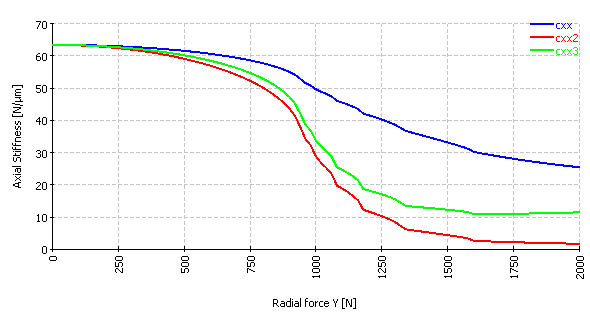
青色の曲線は、5 * 5剛性マトリックスの主対角線です。 赤い曲線は、5 * 5コンプライアンス行列の主対角線の逆数です。 緑色の曲線は、回転なしで移動の自由度のみを考慮した3 * 3コンプライアンス行列の主対角線の逆数です。
ラジアル剛性の場合、異なる剛性値の間には10倍の違いが見られます。 ほとんどの場合、赤い曲線は関連するケースではありませんが、青と緑の曲線の違いもかなり大きいです。 ラジアル剛性の3つの例として、青い曲線は固定された予圧の元でのアンギュラ玉軸受にフィットし、緑の線はバネの予圧を持つアンギュラ玉軸受に適合し、軸方向の予圧のない赤い曲線の定義はトラックローラーに敵しています 。
よって一般的には、軸受の全剛性マトリックスが考慮されるべきであり、荷重に依存し、速度にも依存します。


